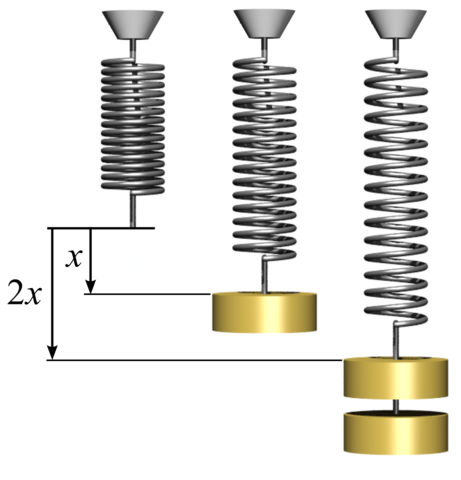
- Coils and rubber bands have a natural size
- If you apply a force to them, they expand
- What is the relation between the expansion and the force?
December 3, 2019
Coils and Rubber bands
Results
| id | rep | N | x1 | x2 | y1 | y2 | src |
|---|---|---|---|---|---|---|---|
| 1 | a | 1 | 360 | 461.0 | 478.0 | 600.0 | andres |
| 2 | a | 1 | 360 | 470.0 | 489.0 | 630.0 | andres |
| 3 | a | 1 | 350 | 461.0 | 480.0 | 620.0 | andres |
| 4 | a | 1 | 350 | 470.0 | 490.0 | 650.0 | andres |
| 5 | a | 1 | 350 | 451.0 | 470.0 | 590.0 | andres |
| 1 | b | 1 | 360 | 460.0 | 479.0 | 600.0 | andres |
| 2 | b | 1 | 360 | 470.0 | 488.0 | 630.0 | andres |
| 3 | b | 1 | 350 | 460.0 | 479.0 | 620.0 | andres |
| 4 | b | 1 | 350 | 470.0 | 489.0 | 650.0 | andres |
| 5 | b | 1 | 350 | 450.0 | 470.0 | 590.0 | andres |
| 1 | c | 1 | 360 | 460.0 | 479.0 | 600.0 | andres |
| 2 | c | 1 | 360 | 470.0 | 490.0 | 630.0 | andres |
| 3 | c | 1 | 350 | 460.0 | 479.0 | 620.0 | andres |
| 4 | c | 1 | 350 | 469.0 | 488.0 | 650.0 | andres |
| 5 | c | 1 | 350 | 450.0 | 469.0 | 590.0 | andres |
| 1 | a | 2 | 360 | 475.0 | 493.0 | 601.0 | andres |
| 2 | a | 2 | 360 | 493.0 | 512.0 | 630.0 | andres |
| 3 | a | 2 | 350 | 490.0 | 508.0 | 620.0 | andres |
| 4 | a | 2 | 350 | 502.0 | 520.0 | 650.0 | andres |
| 5 | a | 2 | 350 | 459.0 | 477.0 | 590.0 | andres |
| 1 | b | 2 | 360 | 495.0 | 492.0 | 600.0 | andres |
| 2 | b | 2 | 350 | 483.0 | 501.0 | 620.0 | andres |
| 3 | b | 2 | 330 | 463.0 | 481.0 | 600.0 | andres |
| 4 | b | 2 | 330 | 481.0 | 498.0 | 630.0 | andres |
| 5 | b | 2 | 340 | 452.0 | 472.0 | 580.0 | andres |
| 1 | c | 2 | 360 | 475.0 | 493.0 | 600.0 | andres |
| 2 | c | 2 | 350 | 483.0 | 502.0 | 620.0 | andres |
| 3 | c | 2 | 330 | 464.0 | 483.0 | 600.0 | andres |
| 4 | c | 2 | 330 | 481.0 | 500.0 | 630.0 | andres |
| 5 | c | 2 | 340 | 455.0 | 473.0 | 580.0 | andres |
| 1 | a | 1 | 40 | 125.0 | 143.0 | 225.0 | 185a34 |
| 2 | a | 1 | 50 | 155.0 | 175.0 | 280.0 | 185a34 |
| 3 | a | 1 | 40 | 195.0 | 215.0 | 375.0 | 185a34 |
| 4 | a | 1 | 10 | 192.0 | 212.0 | 400.0 | 185a34 |
| 5 | a | 1 | 110 | 258.0 | 278.0 | 435.0 | 185a34 |
| 1 | b | 1 | 40 | 125.0 | 143.0 | 225.0 | 185a34 |
| 2 | b | 1 | 50 | 156.0 | 174.0 | 280.0 | 185a34 |
| 3 | b | 1 | 40 | 156.0 | 175.0 | 375.0 | 185a34 |
| 4 | b | 1 | 10 | 238.0 | 258.0 | 400.0 | 185a34 |
| 5 | b | 1 | 110 | 261.0 | 281.0 | 435.0 | 185a34 |
| 1 | c | 1 | 40 | 125.0 | 143.0 | 225.0 | 185a34 |
| 2 | c | 1 | 50 | 155.0 | 174.0 | 280.0 | 185a34 |
| 3 | c | 1 | 40 | 196.0 | 214.0 | 375.0 | 185a34 |
| 4 | c | 1 | 10 | 193.0 | 212.0 | 400.0 | 185a34 |
| 5 | c | 1 | 110 | 260.0 | 279.0 | 435.0 | 185a34 |
| 1 | d | 1 | 40 | 124.0 | 143.0 | 225.0 | 185a34 |
| 2 | d | 1 | 50 | 156.0 | 174.0 | 280.0 | 185a34 |
| 3 | d | 1 | 40 | 195.0 | 214.0 | 375.0 | 185a34 |
| 4 | d | 1 | 10 | 193.0 | 212.0 | 400.0 | 185a34 |
| 5 | d | 1 | 110 | 261.0 | 279.0 | 425.0 | 185a34 |
| 1 | a | 2 | 40 | 130.0 | 145.0 | 225.0 | 185a34 |
| 2 | a | 2 | 50 | 167.0 | 186.0 | 280.0 | 185a34 |
| 3 | a | 2 | 40 | 234.0 | 252.0 | 375.0 | 185a34 |
| 4 | a | 2 | 10 | 242.0 | 260.0 | 400.0 | 185a34 |
| 5 | a | 2 | 110 | 299.0 | 313.0 | 435.0 | 185a34 |
| 1 | b | 2 | 40 | 128.0 | 145.0 | 225.0 | 185a34 |
| 2 | b | 2 | 50 | 167.0 | 185.0 | 280.0 | 185a34 |
| 3 | b | 2 | 40 | 235.0 | 254.0 | 375.0 | 185a34 |
| 4 | b | 2 | 10 | 243.0 | 260.0 | 400.0 | 185a34 |
| 5 | b | 2 | 110 | 299.0 | 314.0 | 435.0 | 185a34 |
| 1 | c | 2 | 40 | 130.0 | 144.0 | 225.0 | 185a34 |
| 2 | c | 2 | 50 | 168.0 | 185.0 | 280.0 | 185a34 |
| 3 | c | 2 | 40 | 235.0 | 254.0 | 375.0 | 185a34 |
| 4 | c | 2 | 10 | 242.0 | 261.0 | 400.0 | 185a34 |
| 5 | c | 2 | 110 | 298.0 | 313.0 | 435.0 | 185a34 |
| 1 | d | 2 | 40 | 130.0 | 144.0 | 225.0 | 185a34 |
| 2 | d | 2 | 50 | 167.0 | 186.0 | 280.0 | 185a34 |
| 3 | d | 2 | 40 | 235.0 | 253.0 | 375.0 | 185a34 |
| 4 | d | 2 | 10 | 243.0 | 260.0 | 400.0 | 185a34 |
| 5 | s | 2 | 110 | 298.0 | 313.0 | 435.0 | 185a34 |
| 1 | a | 1 | 171 | 180.0 | 182.0 | 188.0 | 1e4a6e |
| 2 | a | 1 | 184 | 176.0 | 181.0 | 208.0 | 1e4a6e |
| 3 | a | 1 | 188 | 195.0 | 191.0 | 212.0 | 1e4a6e |
| 5 | a | 1 | 179 | 180.0 | 177.0 | 205.0 | 1e4a6e |
| 1 | b | 2 | 191 | 195.0 | 202.0 | 199.0 | 1e4a6e |
| 2 | b | 2 | 190 | 192.0 | 189.0 | 205.0 | 1e4a6e |
| 3 | b | 2 | 191 | 194.0 | 207.0 | 214.0 | 1e4a6e |
| 4 | b | 2 | 210 | 208.0 | 210.0 | 222.0 | 1e4a6e |
| 5 | b | 2 | 220 | 217.0 | 205.0 | 206.0 | 1e4a6e |
| 1 | c | 2 | 191 | 195.0 | 202.0 | 211.0 | 1e4a6e |
| 2 | c | 2 | 190 | 192.0 | 189.0 | 202.0 | 1e4a6e |
| 3 | c | 2 | 191 | 194.0 | 207.0 | 205.0 | 1e4a6e |
| 4 | c | 2 | 210 | 208.0 | 210.0 | 212.0 | 1e4a6e |
| 5 | c | 2 | 220 | 217.0 | 205.0 | 207.0 | 1e4a6e |
| 1 | a | 2 | 40 | 15.7 | 13.0 | 11.3 | 3b2b4b |
| 2 | a | 2 | 50 | 21.3 | 15.0 | 13.7 | 3b2b4b |
| 3 | a | 2 | 60 | 25.0 | 18.8 | 16.2 | 3b2b4b |
| 4 | a | 2 | 70 | 28.8 | 21.8 | 19.4 | 3b2b4b |
| 5 | a | 2 | 80 | 32.2 | 25.2 | 22.8 | 3b2b4b |
| 1 | b | 2 | 40 | 15.7 | 12.9 | 11.4 | 3b2b4b |
| 2 | b | 2 | 50 | 20.7 | 15.7 | 13.6 | 3b2b4b |
| 3 | b | 2 | 60 | 24.8 | 18.5 | 16.6 | 3b2b4b |
| 4 | b | 2 | 70 | 28.9 | 21.7 | 19.2 | 3b2b4b |
| 5 | b | 2 | 80 | 32.1 | 25.3 | 22.6 | 3b2b4b |
| 1 | c | 2 | 40 | 15.8 | 12.9 | 11.3 | 3b2b4b |
| 2 | c | 2 | 50 | 20.5 | 15.7 | 13.8 | 3b2b4b |
| 3 | c | 2 | 60 | 24.3 | 19.3 | 16.4 | 3b2b4b |
| 4 | c | 2 | 70 | 28.7 | 21.9 | 19.4 | 3b2b4b |
| 5 | c | 2 | 80 | 32.3 | 25.3 | 22.4 | 3b2b4b |
| 1 | a | 1 | 150 | 255.0 | 275.0 | 370.0 | 6ed952 |
| 2 | a | 1 | 100 | 200.0 | 220.0 | 300.0 | 6ed952 |
| 3 | a | 1 | 200 | 290.0 | 310.0 | 396.0 | 6ed952 |
| 4 | a | 1 | 210 | 305.0 | 325.0 | 410.0 | 6ed952 |
| 5 | a | 1 | 150 | 274.0 | 293.0 | 400.0 | 6ed952 |
| 1 | b | 1 | 150 | 256.0 | 274.0 | 370.0 | 6ed952 |
| 2 | b | 1 | 100 | 192.0 | 210.0 | 300.0 | 6ed952 |
| 3 | b | 1 | 200 | 290.0 | 309.0 | 396.0 | 6ed952 |
| 4 | b | 1 | 210 | 303.0 | 321.0 | 410.0 | 6ed952 |
| 5 | b | 1 | 150 | 275.0 | 293.0 | 400.0 | 6ed952 |
| 1 | c | 1 | 150 | 256.0 | 274.0 | 370.0 | 6ed952 |
| 2 | c | 1 | 100 | 192.0 | 210.0 | 300.0 | 6ed952 |
| 3 | c | 1 | 200 | 290.0 | 309.0 | 396.0 | 6ed952 |
| 4 | c | 1 | 210 | 303.0 | 321.0 | 410.0 | 6ed952 |
| 5 | c | 1 | 150 | 275.0 | 293.0 | 400.0 | 6ed952 |
| 1 | a | 2 | 150 | 260.0 | 282.0 | 370.0 | 6ed952 |
| 2 | a | 2 | 100 | 197.0 | 217.0 | 300.0 | 6ed952 |
| 3 | a | 2 | 200 | 294.0 | 314.0 | 396.0 | 6ed952 |
| 4 | a | 2 | 210 | 307.0 | 326.0 | 410.0 | 6ed952 |
| 5 | a | 2 | 150 | 288.0 | 306.0 | 400.0 | 6ed952 |
| 1 | b | 2 | 150 | 263.0 | 282.0 | 370.0 | 6ed952 |
| 2 | b | 2 | 100 | 197.0 | 217.0 | 300.0 | 6ed952 |
| 3 | b | 2 | 200 | 294.0 | 314.0 | 396.0 | 6ed952 |
| 4 | b | 2 | 210 | 307.0 | 326.0 | 410.0 | 6ed952 |
| 5 | b | 2 | 150 | 288.0 | 306.0 | 400.0 | 6ed952 |
| 1 | c | 2 | 150 | 264.0 | 282.0 | 370.0 | 6ed952 |
| 2 | c | 2 | 100 | 197.0 | 217.0 | 300.0 | 6ed952 |
| 3 | c | 2 | 200 | 294.0 | 314.0 | 396.0 | 6ed952 |
| 4 | c | 2 | 210 | 307.0 | 326.0 | 410.0 | 6ed952 |
| 5 | c | 2 | 150 | 288.0 | 306.0 | 400.0 | 6ed952 |
| 1 | a | 1 | 250 | 346.0 | 370.0 | 475.0 | 7183bd |
| 2 | a | 1 | 250 | 365.0 | 385.0 | 495.0 | 7183bd |
| 3 | a | 1 | 250 | 378.0 | 398.0 | 515.0 | 7183bd |
| 4 | a | 1 | 250 | 365.0 | 384.0 | 495.0 | 7183bd |
| 5 | a | 1 | 250 | 359.0 | 378.0 | 475.0 | 7183bd |
| 1 | b | 1 | 250 | 349.0 | 369.0 | 475.0 | 7183bd |
| 2 | b | 1 | 250 | 350.0 | 370.0 | 495.0 | 7183bd |
| 3 | b | 1 | 250 | 365.0 | 385.0 | 515.0 | 7183bd |
| 4 | b | 1 | 250 | 357.0 | 397.0 | 495.0 | 7183bd |
| 5 | b | 1 | 250 | 349.0 | 369.0 | 475.0 | 7183bd |
| 1 | c | 1 | 250 | 348.0 | 368.0 | 475.0 | 7183bd |
| 2 | c | 1 | 250 | 356.0 | 376.0 | 495.0 | 7183bd |
| 3 | c | 1 | 250 | 364.0 | 384.0 | 515.0 | 7183bd |
| 4 | c | 1 | 250 | 356.0 | 376.0 | 495.0 | 7183bd |
| 7 | c | 1 | 250 | 350.0 | 370.0 | 475.0 | 7183bd |
| 1 | a | 2 | 250 | 365.0 | 385.0 | 475.0 | 7183bd |
| 2 | a | 2 | 250 | 381.0 | 401.0 | 495.0 | 7183bd |
| 3 | a | 2 | 250 | 399.0 | 419.0 | 515.0 | 7183bd |
| 4 | a | 2 | 250 | 397.0 | 417.0 | 495.0 | 7183bd |
| 5 | a | 2 | 250 | 366.0 | 386.0 | 475.0 | 7183bd |
| 1 | b | 2 | 250 | 364.0 | 381.0 | 475.0 | 7183bd |
| 2 | b | 2 | 250 | 376.0 | 396.0 | 495.0 | 7183bd |
| 3 | b | 2 | 250 | 393.0 | 413.0 | 515.0 | 7183bd |
| 4 | b | 2 | 250 | 378.0 | 397.0 | 495.0 | 7183bd |
| 5 | b | 2 | 250 | 360.0 | 380.0 | 475.0 | 7183bd |
| 1 | c | 2 | 250 | 366.0 | 386.0 | 475.0 | 7183bd |
| 2 | c | 2 | 250 | 382.0 | 402.0 | 495.0 | 7183bd |
| 3 | c | 2 | 250 | 392.0 | 412.0 | 515.0 | 7183bd |
| 4 | c | 2 | 250 | 381.0 | 401.0 | 495.0 | 7183bd |
| 5 | c | 2 | 250 | 365.0 | 385.0 | 475.0 | 7183bd |
| 1 | a | 1 | 355 | 356.0 | 372.0 | 416.0 | e3459b |
| 2 | a | 1 | 384 | 450.0 | 380.0 | 382.0 | e3459b |
| 3 | a | 1 | 420 | 446.0 | 740.0 | 775.0 | e3459b |
| 4 | a | 1 | 434 | 442.0 | 775.0 | 670.0 | e3459b |
| 5 | a | 1 | 425 | 460.0 | 755.0 | 759.0 | e3459b |
| 1 | b | 1 | 256 | 290.0 | 632.0 | 705.0 | e3459b |
| 2 | b | 1 | 295 | 306.0 | 630.0 | 650.0 | e3459b |
| 3 | b | 1 | 285 | 296.0 | 630.0 | 660.0 | e3459b |
| 4 | b | 1 | 260 | 280.0 | 650.0 | 680.0 | e3459b |
| 5 | b | 1 | 280 | 350.0 | 700.0 | 720.0 | e3459b |
| 1 | c | 1 | 300 | 290.0 | 725.0 | 733.0 | e3459b |
Add the missing columns
rubber$d1 <- rubber$x2-rubber$x1 rubber$d2 <- rubber$y2-rubber$y1 rubber$mid <- rubber$y1-rubber$x2
| id | rep | N | x1 | x2 | y1 | y2 | src | d1 | d2 | mid |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | a | 1 | 360 | 461 | 478 | 600 | andres | 101 | 122 | 17 |
| 2 | a | 1 | 360 | 470 | 489 | 630 | andres | 110 | 141 | 19 |
| 3 | a | 1 | 350 | 461 | 480 | 620 | andres | 111 | 140 | 19 |
| 4 | a | 1 | 350 | 470 | 490 | 650 | andres | 120 | 160 | 20 |
| 5 | a | 1 | 350 | 451 | 470 | 590 | andres | 101 | 120 | 19 |
| 1 | b | 1 | 360 | 460 | 479 | 600 | andres | 100 | 121 | 19 |
Sample case (src=="185a34" & N==2)
Best-fit line
When data seems to be in a straight line, we can find that line using a linear model
model <- lm(d2 ~ d1, data=rubber,
subset=(src=="185a34" & N==1))
model
Call:
lm(formula = d2 ~ d1, data = rubber, subset = (src == "185a34" &
N == 1))
Coefficients:
(Intercept) d1
35.4505 0.7514
What are the coefficients?
Remember that straight lines can be represented by the formula \[\text{d_2}=A+B\cdot \text{d_1}\] The coefficient \(A\) is the value where the line intercepts the vertical axis
The coefficient \(B\) is how much length goes up when n_marbles increases. This is called slope
In our case \(A\) and \(B\) are
(Intercept) d1 35.4504763 0.7513757
Robert Hooke said it first
Robert Hooke (1635–1703) was an English natural philosopher, architect and polymath.
In 1660, Hooke discovered the law of elasticity which describes the linear variation of tension with extension
“The extension is proportional to the force”
Robert Hooke
Natural philosophy was the study of nature and the physical universe that was dominant before the development of modern science
Polymath (from Greek “having learned much”) is a person whose expertise spans a significant number of different subject areas
Biologist. Hooke used the microscope and was the fists to use the term cell for describing biological organisms.
How do we model a coil?
The essence of the coil is:
- It has a natural length \(L\)
- If we change the length by \(x\), it pulls with a force \[\mathrm{force}(x)= K \cdot (L-x)\]
