Class 21: De Bruijn Assembly

Bioinformatics

Andrés Aravena

23 December 2021

Assembly statistics

Assembly Statistics

When we report an assembly result, we describe

  • Depth of coverage

  • Breadth of coverage

  • Number of contigs

  • N50

Two reads connect when they overlap

We only see overlaps over a threshold \(T\)

The best \(T\) has to be big enough to guarantee that the reads do not overlap by chance

Bigger values of \(T\) reduce the probability of “overlap by chance”

What is the overlap size?

We can simulate in the computer

Negative overlap are gaps

If two reads overlap…

…they are in the same Contig

A group of contiguous sequences is called Contig

The goal of the assembly process is to find one contig.

The sequence of this contig will be the genome

Most of times we do get several contigs

Num. contigs depends on 𝐺, 𝐿, 𝑁 and 𝑇

  • 𝐿 =100
  • 𝐺 =106
  • 𝑇 =20

How many reads shall you pay?

What if reads are longer?

  • 𝐿 =300
  • 𝐺 =106
  • 𝑇 =20

Longer reads are better

This is described in the paper

Lander ES, Waterman MS. Genomic mapping by fingerprinting random clones: a mathematical analysis. Genomics. 1988 Apr; 2(3):231-9. doi: 10.1016/0888-7543(88)90007-9. PMID: 3294162.

lander-waterman

Contig length

With this simulation we can also calculate the length of each contig.

N50

Given a set of contigs, the N50 is defined as the sequence length of the shortest contig at 50% of the total genome length

We sort the contigs from largest to smallest

When do we get 50%?

We identify which contig crosses the 50% line

N50 is the length of that contig

Which contig reach 50% of bases?

sorted_len pct_in_contig cumulative
1981 30.40 30.40
1202 18.44 48.84
1055 16.19 65.03
677 10.39 75.42
581 8.92 84.33
511 7.84 92.17
510 7.83 100.00

Assembly quality

Each fragment has two reads

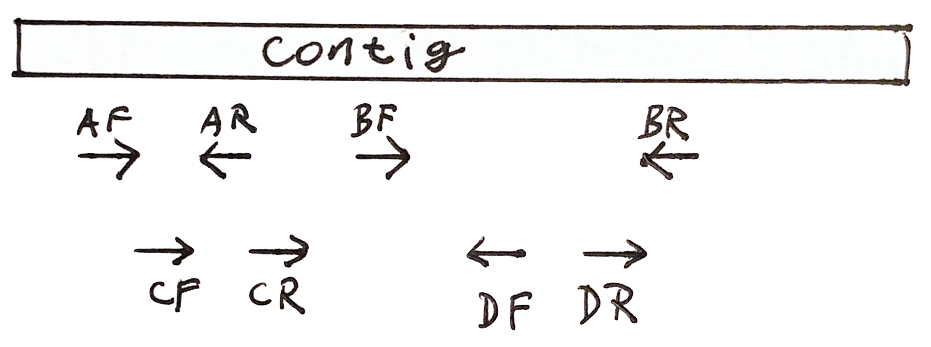
fragments-reads-distances

  • Both reads should point to each other (AF, AR)
  • If they point in the wrong direction, it is bad
  • The distance between both reads should not be too large or too small

Scaffolding

If a fragment has one read in Contig 1 and the other in Contig 2, then we know that the contigs are close

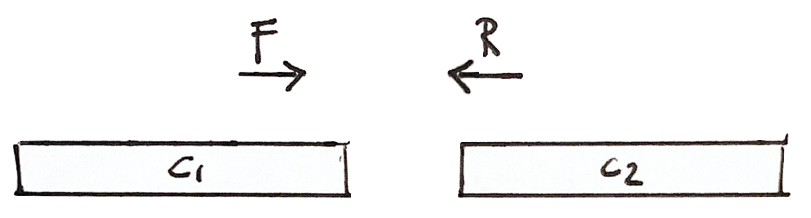
scaffold 1

Scaffolding

More shared fragments gives more confidence to the scaffold

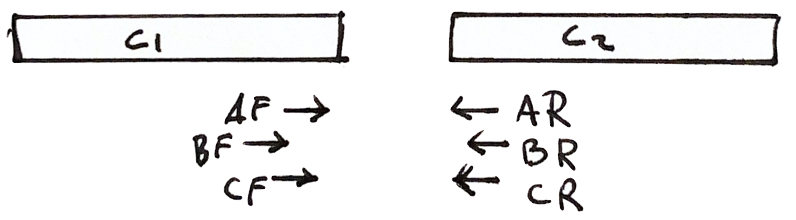
scaffold 2

Scaffolding

Shared fragments allow us to find the relative orientation of contigs, and make a scaffold of contigs and gaps scaffold 3

The problem of Repeats

repeat in real genome

The assembly can be wrong

Given the information we have, there are at least two solutions

repeat two solutions

We cannot do better with the available information

We need more information

To decide the correct one, we need more information

For example, longer reads containing the repeat and its context

long read

Or read pairs from larger fragments, so each read is outside the repeat

Another way to assemble

The problem

Assemblers based on Overlay–Layout–Consensus cannot handle repeats

Moreover, they can handle only a few thousand reads

NGS produces millions of reads, so a different approach was developed

𝑘-mers instead of reads

Since a read has hundreds of bp, it can contain part of a repeat

It is better to use shorter sequences (𝑘-mers), that are either inside or outside the repeat

𝑘 is typically between 20 and 130, and can be chosen automatically

Each read is translated into a list of 𝑘-mers

ATGCATATATAGCA
ATG       
 TGC      
  GCA     
   CAT    
    ATA   
     TAT  
      ATA 
       TAT
        ATA
         TAG
          AGC
           GCA

We do not count repeated 𝑘-mers

ATGCATATATAGCA
ATG       
 TGC      
  GCA     
   CAT    
    ATA   
     TAT  
         TAG
          AGC
           GCA

De Bruijn’s graphs

Each 𝑘-mer is a node in a directed graph

Two nodes are connected if the last (𝑘-1) bp of the first 𝑘-mer are the same as the first (𝑘-1) bp of the second one

ATGCATATATAGCA
ATG TGC GCA CAT ATA TAT TAG AGC GCA

We get an honest assembly

This approach does not solve the repeats

Instead, it shows the repeats clearly

repeat all solutions

This way we know what are the issues, and we can design an experiment (PCR?) to solve them

Repeats result in a funny graph

Source: https://github.com/rrwick/Unicycler

Output format: FASTG

Like FAST, but showing also the graph structure. For example

>EDGE_641517_length_474_cov_1.855908;
AACACTGATTGCCTCCCCCCCGTTGATGGGTAAAATAGCCGCAATTTTTCGTTTTCAACA
[…]
GCTGCCTGATGGTTATCGACGCTGCAAAAGGTGTTGAAGATCGTACCCGTAAGC
>EDGE_621787_length_514_cov_1.860465';
TGTCGATGCGGTGTACATTGTGGCAACGCCGGGTGAAATCGCTTTTATCAAACCGATGAT
[…]
TGGCTGGAAGGCAAAGGACTGCGGTTTATCGCCG
>EDGE_678376_length_822_cov_333.633094:EDGE_679076_length_4092_cov_132.576797',EDGE_679634_length_28752_cov_122.881432;
GGCACTGTTGCAAATAGTCGGTGGTGATAAACTTATCATCCCCTTTTGCTGATGGAGCTG
[…]
AGACAAAAGGCTGCCTCATCGCTAACTTTGCAACAGTGCCGG

Bandage: Look and edit the graph

Bandage is a program to visualize a assembly graph

Example from The New York Times: “Team of Rival Scientists Comes Together to Fight Zika”. March 30, 2016

Online Material