Class 10: Accumulative sums and Systems

Computing for Molecular Biology 2

Andrés Aravena, PhD

2 April 2021

Idea 1:
Accumulative sums

Accumulative sum

Everyday you spend some money

Some days you receive money

How much money you have each day?

Accumulative Sum: daily balance

The income can be positive (salary) or negative (expenses)

The balance on first day is your initial money

The balance of today is the balance of yesterday plus the income of today

balance[today] <- balance[yesterday] + income[today]

Today and yesterday

We will see several “days”, represented by i

It is useful to think that

  • i represents “today”
  • i-1 represents “yesterday”

If we know income, we can calculate balance

The balance on first day is your initial money

balance[1] <- income[1]

The balance of today is the balance of yesterday plus the income of today

for(i in 2:length(income)) {
    balance[i] <- balance[i-1] + income[i]
}

Putting it all together

The input is income, the output is balance

balance <- rep(NA, length(income))

balance[1] <- income[1]

for(i in 2:length(income)) {
    balance[i] <- balance[i-1] + income[i]
}

Remember that we need to create the output vector.

Why is this important?

Life is change

Biology is the study of life

Living organisms change. They are alive

To study life, we need to study how things change

Two vectors

For each thing that we consider, we will carry two vectors

  • One vector representing the state
    • For example, the balance of money
  • One vector representing the change
    • For example, the income/expenses

From change to state

If we know the change vector, we can always know the state vector

state[1] <- change[1]
for(i in 2:length(change)) {
    state[i] <- state[i-1] + change[i]
}

The input is change, the output is state

Idea 2: state and change

Interesting systems

As we said,

If we know the change today, we can know the state today

In real life, in particular in biology, we do not know the change until we know the state

If we know the state yesterday, we can know the change today

We will unlock this cycle

We will calculate change and state at the same time

A simple system: growing cell lines

In a Petri dish we have one cell

Every hour, 10% of the cells duplicate, and they never die

How many cells we have after i hours?

(this is a toy problem, to start thinking)

In a drawing

Duplication process takes one cell and delivers two cells

The parts of the system

There is only one element: the cells

There are two values important to them:

  • The number of cells
  • The change in the number of cells

Let’s give them names

The vector cells is the number of cells

The value cells[i] is the number of cells on time i

The vector growth is the growth of the number of cells

There are growth[i] new cells between time i-1 and i

Every hour, 10% of the cells duplicate

The duplication_rate is 0.1

growth[i] <- cells[i-1]*duplication_rate

The growth on time i depends on the cells existing on time i-1

The number of cells increases

cells will be the cumulative sum of growth

But growth depends on cells

Therefore, we calculate both together

How many cells after one week?

One week has 168 hours

for(i in 2:168) {
    growth[i] <- cells[i-1]*duplication_rate
    cells[i]  <- cells[i-1] + growth[i]
}

Solving the system

Let’s simulate for one week

First we create empty vectors to store the result

cells <- rep(NA, 168)
growth <- rep(NA, 168)

Then we start with 1 cell/cm2 and zero growth

cells[1] <- 1
growth[1] <- 0

One week passes

How many cells we have after 168 hours?

cells <- rep(NA, 168)
growth <- rep(NA, 168)

duplication_rate <- 0.1

cells[1]  <- 1
growth[1] <- 0

for(i in 2:168) {
    growth[i] <- cells[i-1]*duplication_rate
    cells[i]  <- cells[i-1] + growth[i]
}

Now we have the vector cells. We can look at cells[168]

We can plot cells for each hour

This is Exponential Growth

Number of cells increases 10% every hour

That is, it duplicates every 7:15 hours

Number of cells increases 10 times every ≈24h

In one week their volume is 80ml

In two weeks their volume is 670 cubic meters

All code will have the same shape

petri_dish <- function(N, duplication_rate) {
  # create empty vectors of size N
  cells <- rep(NA, N)
  growth <- rep(NA, N)
  # Store the initial state in [1]
  cells[1]  <- 1
  growth[1] <- 0
  for(i in 2:N) {
    growth[i] <- cells[i-1]*duplication_rate
    cells[i]  <- cells[i-1] + growth[i]
  }
  return(data.frame(cells, growth))
}

Limited food

In practice cells never grow that much

There is a limited amount of food

So we need to include food in the system

How can we include food in the system?

And, what is a system?

Systems

Basic Systems Theory

These ideas are useful to understand the reality

A System is a set of parts that interact

Each part can be a smaller system

The behavior of the system depends on the parts AND on the interactions

Total is bigger than the sum of the parts

Complex systems can have emergent properties

That is, the system can do things that the parts cannot do

The system is different from the parts

Drawing Systems

We will represent any system with a network with two kinds of nodes

  • Circles will represent items
  • Boxes will represent processes

Circles are connected to boxes with arrows and vice-versa

Arrows

  • Circles are connected to boxes

  • Boxes are connected to circles

  • There cannot be arrows between circles or between boxes
    (only between nodes of different shape)

  • There can be more than one arrow between a box and a circle, in any direction

The technical name of this kind of network is directed bipartite multigraph

Example: Molecular Biology’s Dogma

  • Which are the items?
  • Which are the processes?

System of cells and food

Cells eat food, food limits growth rate

Let’s say that initially food is 20 ng

More cells eat more food, limited by the eat rate

We assume that when a cell gets food, it divides

Cells eat food, food limits growth rate

Let’s say that initially food[1] <- 20

More cells eat more food, limited by the eat_rate:

food_change[i] <- -cells[i-1]*food[i-1]*eat_rate

We assume that when a cell gets food, it divides:

growth[i] <- cells[i-1]*food[i-1]*eat_rate

What happens now?

All the code together

cells <- growth      <- rep(NA, 168)
food  <- food_change <- rep(NA, 168)
cells[1]       <- 1
growth[1]      <- 0
food[1]        <- 20
food_change[1] <- 0
eat_rate <- 0.003
for(i in 2:168) {
  growth[i]      <-  cells[i-1]*food[i-1]*eat_rate
  food_change[i] <- -cells[i-1]*food[i-1]*eat_rate
  cells[i] <- cells[i-1] + growth[i]
  food[i]  <-  food[i-1] + food_change[i]
}

Result

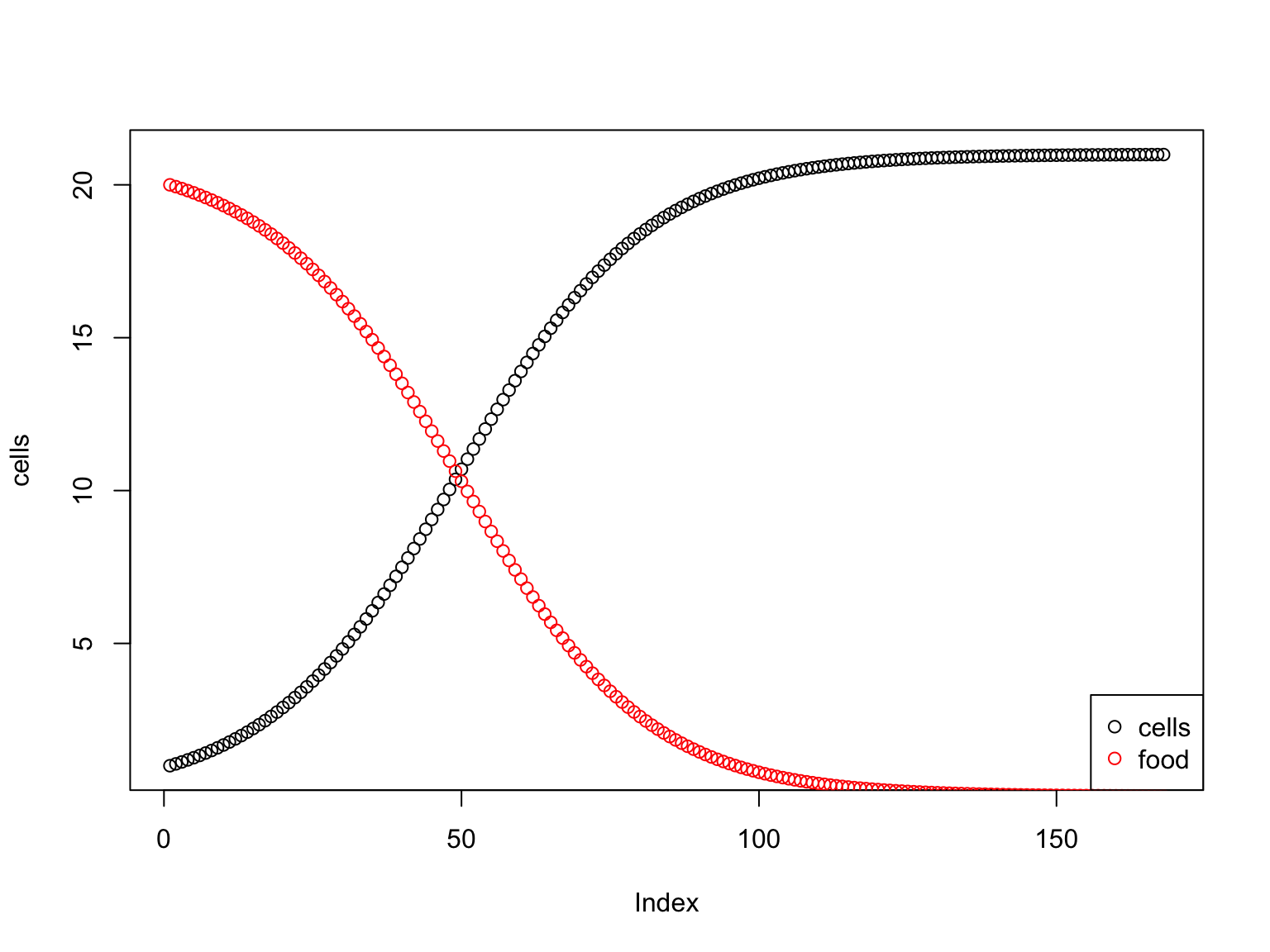
Homework

Read The Biologist Toolbox: Drawing Systems

Explain —in English— what happens in the system represented by this drawing