Class 4: Global and Local Alignment
Bioinformatics
Andrés Aravena
October 26, 2023
Previous class
- Hamming distance
- Levenstein distance
- Dot plot
Dot plot
We have two sequences. Lets give them names
- Query sequence in the rows
- Subject sequence in the columns
The idea is to draw a rectangle
Mark cells where row and column letters are equal
It looks like this

The goal is to move from one corner to the other
Jumping black to black is free
Horizontal and vertical moves are gaps
We move from one corner to the other
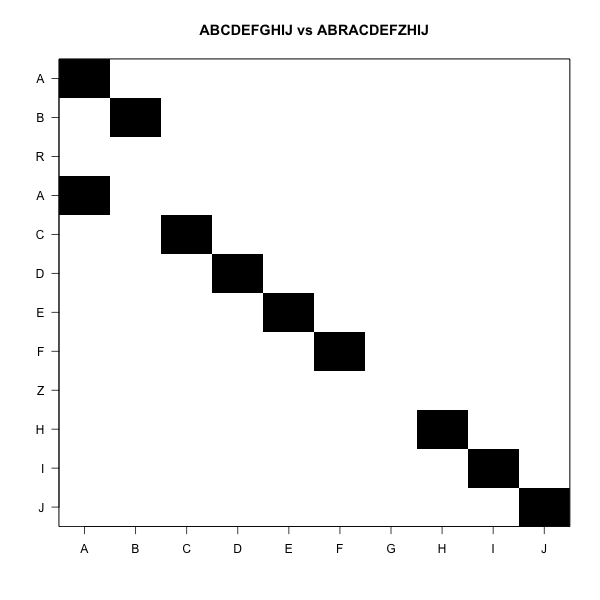
White blocks add to the distance
This matrix is \(D\) with cells \(D_{i,j}\)
There are two questions
- What is the Levenshtein distance
- That is, the length of the shortest path
- What is the optimal alignment
- That is, what is the shortest path
The first question is easy and has only one answer
The second question is harder and can have many answers
Calculating the score
Levenshtein distance is easy to calculate from the dot plot
We build a second matrix where each cell \(M_{i,j}\) has the smallest number of changes we need to align the query \((q_1,…,q_i)\) to the subject \((s_1,…,s_j)\)
Building the matrix
There are three ways to get to \(M_{i,j}\)
- In diagonal from \(M_{i-1,j-1},\) and there may be a mismatch
- Horizontally from \(M_{i,j-1}\) with a gap
- Vertically from \(M_{i-1,j}\) with a gap
Formula
\[M_{i,j} = \min\begin{cases} M_{i-1,j-1} & \text{if }q_i\not=s_j \text{ (match)}\\ M_{i-1,j-1} + 1 & \text{if }q_i\not=s_j \text{ (mismatch)}\\ M_{i-1,j} + 1 & \text{(gap in subject)} \\ M_{i,j-1} + 1 & \text{(gap in query)} \end{cases}\]
Initial gaps
We need to include an extra row at the beginning of the matrix \(M\)
\[\begin{aligned}M_{i,0} &= i \qquad \text{ for each }i\in\{1,…,m\}\\ M_{0,j} &= j \qquad \text{ for each } j\in\{1,…,n\}\end{aligned}\]
Partial matching
Levenstein distance is Global Alignment
Useful to compare proteins
But not good when we look for a gene in a genome
or a domain in a protein
What shall we do when the query is much smaller than all subjects?
Semi-global alignment
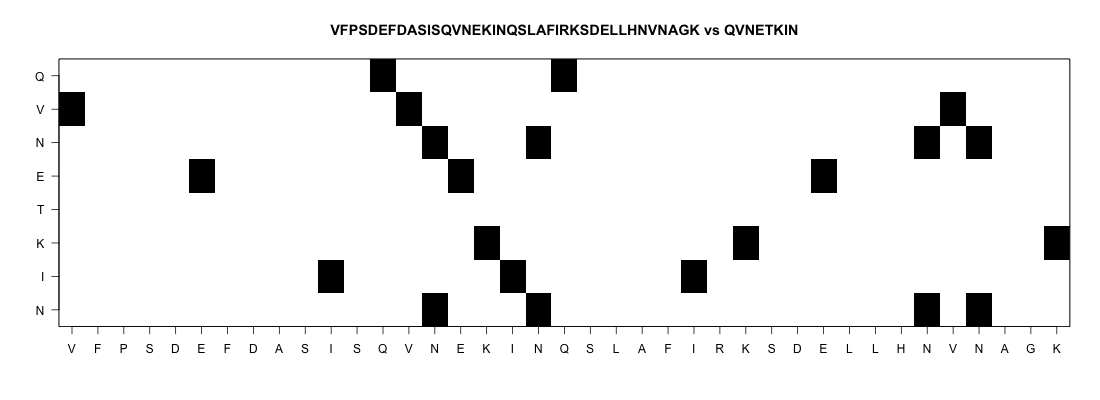
In this case we want to go from one side to the other
Gaps in semi-global alignment
The query is much smaller than the subject
In this case we distinguish two kind of gaps
Internal gaps, inside the sequences
External gaps, outside the query sequence
External gaps do not count
External gaps are caused by the experiment
Example: PCR cuts part of a genome
The query is the sequence between primers
Anything outside the query cannot be seen for technical reasons
Internal gaps do count
Internal gaps are caused by nature
They are gained or lost during replication
They have biological meaning
Therefore, they must be counted
Initial gaps in Semi-global alignment
This time the first row is 0, because external gaps are free
\(M_{i,0} = i\) for each \(i\in\{1,…,m\}\)
\(M_{0,j} = 0\) for each \(j\in\{1,…,n\}\)
And we look for the smallest value in the last row
Kinds of alignments
Different alignments for different questions
- Global alignment compares genes to genes, or
proteins to proteins
- We expect that both sequences are similar
- Semi-global alignment compares genes to genomes
- We expect that query is similar to part of subject
- Local alignment compares genomes to genomes
- We expect that part of the query is similar to part of subject
Global alignment
- All sequences must match.
- Each gap is penalized
Semi-global alignment
- All sequences must match
- One may be shorter than the other.
- External gaps are not penalized
- Internal gaps are penalized
Local alignment
- Some part of the sequence must match
- External gaps are not penalized
- Can be with or without internal gaps
Global v/s local

Part of query to part of subject
ABRACADABRA
CHUPACABRAExternal gaps do not count
ABRACADABRA
||||
CHUPACABRALocal alignment is not a distance
Since external gaps do not count, we can always use them
In this case the smallest distance is always 0
The smallest cost is achieved taking one letter
ABRACADABRA
|
CHUPACABRAWe cannot make it a minimization problem
Score instead of distance
Instead of finding a minimum, we look for a maximum
- Matching places get positive score
- Mismatch and gaps get negative score
The philosophy is the same, but we look for big numbers instead of small numbers
Dot plot becomes a matrix
Initially we placed 1 or 0 on each cell depending on match or mismatch
Now we put positive or negative numbers, depending of single-letter scores
Substitution scoring matrices
Single-letter scores (example)
If we pair two letters \(x\) and \(y\), we need to know how they contribute to the score value. For example,
- If \(x = y\) the score increases by 1
- If \(x ≠ y\) the score decreases by 2
- If one of the letters is
-(a gap), the score reduces by 4
In general, we have a substitution scoring matrix \(C_{x, y}\) for each \(x\) and \(y\)
Single-letter scores
In one equation
\[C_{x, y} = \begin{cases} +1 & \quad \text{if } x=y\\ -2 & \quad \text{if } x≠y\\ -4 & \quad \text{if } x=\texttt{"-"} \\ -4 & \quad \text{if }y=\texttt{"-"} \end{cases}\]
Substitution Scoring matrices
The Substitution Scoring Matrix has one row and one column for each letter in our alphabet
For example 4 rows and 4 columns for DNA sequences
In DNA it is common to have +1 for match and -2 for mismatch
Sometimes we can use (+1,-3), (+1,-1) or even (4,-5)
DNA substitution matrix
A C G T -
A 1 -2 -2 -2 -4
C -2 1 -2 -2 -4
G -2 -2 1 -2 -4
T -2 -2 -2 1 -4
- -4 -4 -4 -4 -4Amino-acid substitution matrices
In proteins the alphabet has 20 letters, so the scoring matrix is 20×20
The scores of these matrices are based on the relative frequency of each mutation in nature
Obviously, we only care about non-lethal mutations
More specifically, we care about the Point Mutations that are Accepted
These are called PAM matrices (Margaret Dayhoff, 1978)
Accepted Mutation matrices
Based on 1572 mutations in 71 families of closely related proteins
Dayhoff only used alignments having at least 85% identity
She assumed that any aligned mismatches were the result of a single mutation event, rather than several at the same location
PAM matrices
PAM1 is the scoring matrix for proteins in a “short” period
With some easy mathematics we can calculate PAM2, PAM30, PAM250, etc
They represent mutations in 2, 30, and 250 short periods
PAM30 matrix
A R N D C Q E G H I L K M F P S T W Y V B J Z X *
A 6 -7 -4 -3 -6 -4 -2 -2 -7 -5 -6 -7 -5 -8 -2 0 -1 -13 -8 -2 -3 -6 -3 -1 -17
R -7 8 -6 -10 -8 -2 -9 -9 -2 -5 -8 0 -4 -9 -4 -3 -6 -2 -10 -8 -7 -7 -4 -1 -17
N -4 -6 8 2 -11 -3 -2 -3 0 -5 -7 -1 -9 -9 -6 0 -2 -8 -4 -8 6 -6 -3 -1 -17
D -3 -10 2 8 -14 -2 2 -3 -4 -7 -12 -4 -11 -15 -8 -4 -5 -15 -11 -8 6 -10 1 -1 -17
C -6 -8 -11 -14 10 -14 -14 -9 -7 -6 -15 -14 -13 -13 -8 -3 -8 -15 -4 -6 -12 -9 -14 -1 -17
Q -4 -2 -3 -2 -14 8 1 -7 1 -8 -5 -3 -4 -13 -3 -5 -5 -13 -12 -7 -3 -5 6 -1 -17
E -2 -9 -2 2 -14 1 8 -4 -5 -5 -9 -4 -7 -14 -5 -4 -6 -17 -8 -6 1 -7 6 -1 -17
G -2 -9 -3 -3 -9 -7 -4 6 -9 -11 -10 -7 -8 -9 -6 -2 -6 -15 -14 -5 -3 -10 -5 -1 -17
H -7 -2 0 -4 -7 1 -5 -9 9 -9 -6 -6 -10 -6 -4 -6 -7 -7 -3 -6 -1 -7 -1 -1 -17
I -5 -5 -5 -7 -6 -8 -5 -11 -9 8 -1 -6 -1 -2 -8 -7 -2 -14 -6 2 -6 5 -6 -1 -17
L -6 -8 -7 -12 -15 -5 -9 -10 -6 -1 7 -8 1 -3 -7 -8 -7 -6 -7 -2 -9 6 -7 -1 -17
K -7 0 -1 -4 -14 -3 -4 -7 -6 -6 -8 7 -2 -14 -6 -4 -3 -12 -9 -9 -2 -7 -4 -1 -17
M -5 -4 -9 -11 -13 -4 -7 -8 -10 -1 1 -2 11 -4 -8 -5 -4 -13 -11 -1 -10 0 -5 -1 -17
F -8 -9 -9 -15 -13 -13 -14 -9 -6 -2 -3 -14 -4 9 -10 -6 -9 -4 2 -8 -10 -2 -13 -1 -17
P -2 -4 -6 -8 -8 -3 -5 -6 -4 -8 -7 -6 -8 -10 8 -2 -4 -14 -13 -6 -7 -7 -4 -1 -17
S 0 -3 0 -4 -3 -5 -4 -2 -6 -7 -8 -4 -5 -6 -2 6 0 -5 -7 -6 -1 -8 -5 -1 -17
T -1 -6 -2 -5 -8 -5 -6 -6 -7 -2 -7 -3 -4 -9 -4 0 7 -13 -6 -3 -3 -5 -6 -1 -17
W -13 -2 -8 -15 -15 -13 -17 -15 -7 -14 -6 -12 -13 -4 -14 -5 -13 13 -5 -15 -10 -7 -14 -1 -17
Y -8 -10 -4 -11 -4 -12 -8 -14 -3 -6 -7 -9 -11 2 -13 -7 -6 -5 10 -7 -6 -7 -9 -1 -17
V -2 -8 -8 -8 -6 -7 -6 -5 -6 2 -2 -9 -1 -8 -6 -6 -3 -15 -7 7 -8 0 -6 -1 -17
B -3 -7 6 6 -12 -3 1 -3 -1 -6 -9 -2 -10 -10 -7 -1 -3 -10 -6 -8 6 -8 0 -1 -17
J -6 -7 -6 -10 -9 -5 -7 -10 -7 5 6 -7 0 -2 -7 -8 -5 -7 -7 0 -8 6 -6 -1 -17
Z -3 -4 -3 1 -14 6 6 -5 -1 -6 -7 -4 -5 -13 -4 -5 -6 -14 -9 -6 0 -6 6 -1 -17
X -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -17
* -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 -17 1BLOSUM matrices
Using local alignment we can identify conserved regions
In 1992 Steven Henikoff and Jorja Henikoff created new substitution matrices based on local alignment of blocks
BLOcks SUbstitution Matrix
Idea: each protein domain can evolve at different speeds
BLOSUM62
A R N D C Q E G H I L K M F P S T W Y V B J Z X *
A 4 -1 -2 -2 0 -1 -1 0 -2 -1 -1 -1 -1 -2 -1 1 0 -3 -2 0 -2 -1 -1 -1 -4
R -1 5 0 -2 -3 1 0 -2 0 -3 -2 2 -1 -3 -2 -1 -1 -3 -2 -3 -1 -2 0 -1 -4
N -2 0 6 1 -3 0 0 0 1 -3 -3 0 -2 -3 -2 1 0 -4 -2 -3 4 -3 0 -1 -4
D -2 -2 1 6 -3 0 2 -1 -1 -3 -4 -1 -3 -3 -1 0 -1 -4 -3 -3 4 -3 1 -1 -4
C 0 -3 -3 -3 9 -3 -4 -3 -3 -1 -1 -3 -1 -2 -3 -1 -1 -2 -2 -1 -3 -1 -3 -1 -4
Q -1 1 0 0 -3 5 2 -2 0 -3 -2 1 0 -3 -1 0 -1 -2 -1 -2 0 -2 4 -1 -4
E -1 0 0 2 -4 2 5 -2 0 -3 -3 1 -2 -3 -1 0 -1 -3 -2 -2 1 -3 4 -1 -4
G 0 -2 0 -1 -3 -2 -2 6 -2 -4 -4 -2 -3 -3 -2 0 -2 -2 -3 -3 -1 -4 -2 -1 -4
H -2 0 1 -1 -3 0 0 -2 8 -3 -3 -1 -2 -1 -2 -1 -2 -2 2 -3 0 -3 0 -1 -4
I -1 -3 -3 -3 -1 -3 -3 -4 -3 4 2 -3 1 0 -3 -2 -1 -3 -1 3 -3 3 -3 -1 -4
L -1 -2 -3 -4 -1 -2 -3 -4 -3 2 4 -2 2 0 -3 -2 -1 -2 -1 1 -4 3 -3 -1 -4
K -1 2 0 -1 -3 1 1 -2 -1 -3 -2 5 -1 -3 -1 0 -1 -3 -2 -2 0 -3 1 -1 -4
M -1 -1 -2 -3 -1 0 -2 -3 -2 1 2 -1 5 0 -2 -1 -1 -1 -1 1 -3 2 -1 -1 -4
F -2 -3 -3 -3 -2 -3 -3 -3 -1 0 0 -3 0 6 -4 -2 -2 1 3 -1 -3 0 -3 -1 -4
P -1 -2 -2 -1 -3 -1 -1 -2 -2 -3 -3 -1 -2 -4 7 -1 -1 -4 -3 -2 -2 -3 -1 -1 -4
S 1 -1 1 0 -1 0 0 0 -1 -2 -2 0 -1 -2 -1 4 1 -3 -2 -2 0 -2 0 -1 -4
T 0 -1 0 -1 -1 -1 -1 -2 -2 -1 -1 -1 -1 -2 -1 1 5 -2 -2 0 -1 -1 -1 -1 -4
W -3 -3 -4 -4 -2 -2 -3 -2 -2 -3 -2 -3 -1 1 -4 -3 -2 11 2 -3 -4 -2 -2 -1 -4
Y -2 -2 -2 -3 -2 -1 -2 -3 2 -1 -1 -2 -1 3 -3 -2 -2 2 7 -1 -3 -1 -2 -1 -4
V 0 -3 -3 -3 -1 -2 -2 -3 -3 3 1 -2 1 -1 -2 -2 0 -3 -1 4 -3 2 -2 -1 -4
B -2 -1 4 4 -3 0 1 -1 0 -3 -4 0 -3 -3 -2 0 -1 -4 -3 -3 4 -3 0 -1 -4
J -1 -2 -3 -3 -1 -2 -3 -4 -3 3 3 -3 2 0 -3 -2 -1 -2 -1 2 -3 3 -3 -1 -4
Z -1 0 0 1 -3 4 4 -2 0 -3 -3 1 -1 -3 -1 0 -1 -2 -2 -2 0 -3 4 -1 -4
X -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -4
* -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 1