Class 5: Finding Local Alignments
Bioinformatics
Andrés Aravena
November 2, 2022
In the previous classes
- Hamming distance: count mismatches
- Levenstein distance: count mismatches and indels
- Dot plots
- Global and semi-global alignment
Different questions need different alignments
Different alignments for different questions
- Global alignment compares genes to genes, or
proteins to proteins
- We expect that both sequences are similar
- Semi-global alignment compares genes to genomes
- We expect that query is similar to part of subject
- Local alignment compares genomes to genomes
- We expect that part of the query is similar to part of subject
Global, Semi-Global and Local alignment
- Global
- all sequences must match.
- Each gap is penalized
- Semi-global
- all sequences must match, but one may be shorter than the other.
- external gaps are not penalized
- Local
- Some part of the sequence must match
- external gaps are not penalized
- can be with or without internal gaps
Global v/s local

Wikipedia
Part of query to part of subject
ABRACADABRA
CHUPACABRAWe have two alignments
ABRACADABRA ABRACADABRA
|||| ||||
CHUPACABRA CHUPACABRAExternal gaps do not count
Dot plots show the alignments
Here there is no alignment
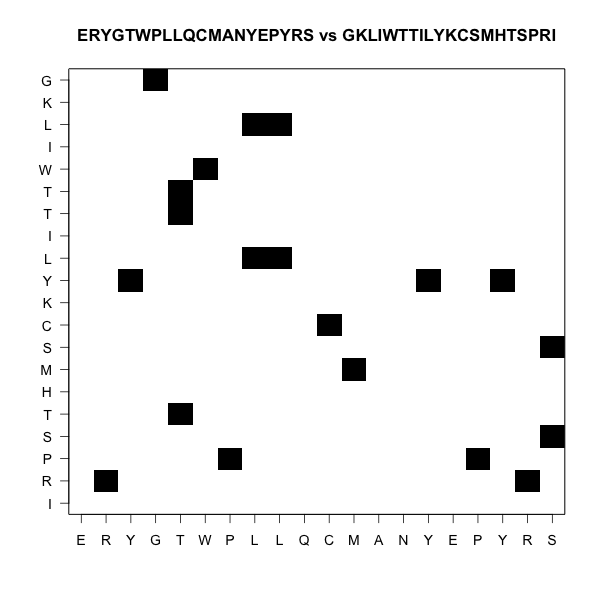
One ungapped alignment
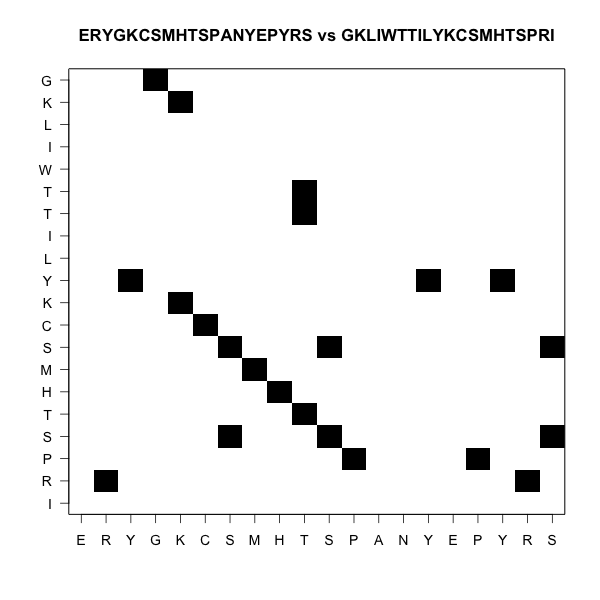
Two ungapped alignments, or one gapped
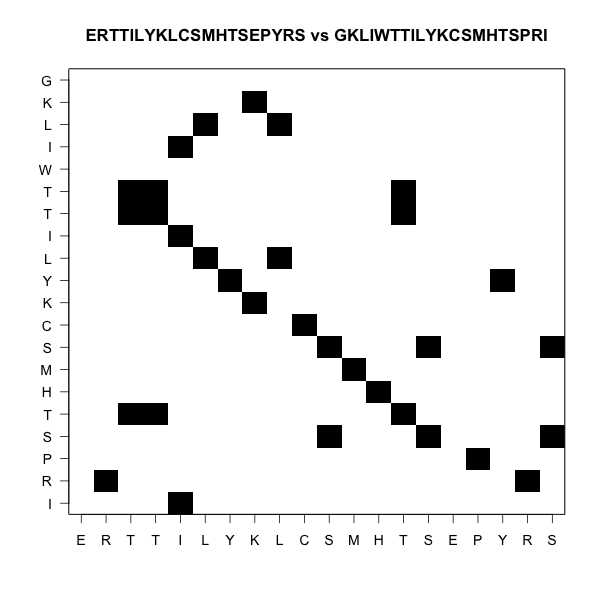
Looking the diagonals
For local alignment we have two cases
- Ungapped, where we can only move in diagonal
- Gapped, where we can move diagonal, horizontal, and vertical
- Horizontal and vertical movement gives gaps
Global and semi-global alignments always have gaps
Local alignment is not like global alignment
We found global alignment using distances
“Distance” means that smaller numbers are better
If the distance is 0, then the two sequences are identical
If the distance is small, the two sequences are similar
If the distance is big, the sequences are different
Local alignment is not a distance
Since external gaps do not count, we can always use them
In this case the smallest distance is always 0
The smallest cost is achieved taking one letter
ABRACADABRA
|
CHUPACABRAWe cannot find local alignments using small values
(it is not a minimization problem)
Score instead of distance
Instead of finding a minimum, we look for a maximum
- Matching places get positive score
- Mismatch and gaps get negative score
The philosophy is the same, but we look for big numbers instead of small numbers
We look for the Optimal Alignment
Dot plot becomes a matrix
Initially we placed 1 or 0 on each cell depending on match or mismatch
Now we put positive or negative numbers, depending of single-letter scores
\[D_{i,j} = \text{Score}(q_i,s_j)\]
We can find optimal alignment efficiently
Once the “dot plot matrix” is complete, it is easy to find the optimal score
Global alignment: find the largest sum from corner to corner
Semi-global alignment: find the largest sum from side to side
Local alignment: find the largest sum in any diagonal
Local alignment score formula
We have three options as before, but not negative values
\[M_{i,j} = \max\begin{cases} M_{i-1,j-1} + \text{Score}(q_i,s_j)\\ M_{i-1,j} + \text{gap} \\ M_{i,j -1} + \text{gap}\\ 0\end{cases}\]
Notice we use \(\max\) instead of \(\min\)
Gaps
Gap penalty
We prefer this alignment
GGGTAACCTACCTC
||| ||||| ||||
GGGCAACCTGCCTCinstead of this other alignment
GGGT-AACCTA-CCTC
||| ||||| ||||
GGG-CAACCT-GCCTCThus, gap penalty must be greater than mismatch penalty
Long gaps instead of short ones
We prefer this alignment
TCAAAGAG---GATA
||| ||| ||||
TCA--GAGGGGGATAinstead of this other alignment
TCAAAGA-G-G-ATA
|| | || | | |||
TC-A-GAGGGGGATAWe want few long gaps instead of many short gaps
Affine gaps
Gap values must reflect how real insertions and deletions occur in nature
We observe that, once an indel event starts, it can easily grow
If the polymerase jumps, then it can jump a long distance
To represent this, we use affine gaps
Linear v/s affine
So far we considered only linear gaps
The penalty of \(n\) consecutive
gaps is \(n\cdot G\)
(\(G\) is the gap penalty)
Now we consider affine gaps, where the first gap is expensive, but the consecutive are cheap
The penalty of \(n\) consecutive gaps is \(I + n\cdot E\)
\(I\) is the initial gap penalty, \(E\) is the gap extension penalty
BLAST
BLAST
The most common tool for local alignment is BLAST
Basic Local Alignment Search Tool
BLAST is not Global Alignment
Using BLAST
There are two ways of using BLAST
- Going to NCBI’s website: https://blast.ncbi.nlm.nih.gov/
- Runs in NCBI servers with NCBI databases
- Using a command line version
- Runs in your server with your databases
- can also send jobs in NCBI servers with NCBI databases
- Download it from NCBI website
For today we can look at NCBI page
Types of BLAST
Depending on the alphabet of the query and subject
- BlastN
- Search nucleotides in nucleotide databases
- BlastP
- Search proteins in protein databases
There are others. Today we only use these ones
NCBI protein databases
- nr
- Non-redundant protein sequences
- refseq_protein
- Reference proteins
- refseq_select
- Reference Select proteins
There are others. Today we only use these ones
What is “Non-Redundant”?
These databases get data from several sources
Sometimes two people upload the same sequence but with different ID
For example, EMBL ID, GenBank ID, RefSeq ID, etc.
This database combines all identical entries into one, and keeps all the alternative IDs
Let’s test it
Let’s look for Terje Steinum’s data
This is a 16S gene amplified by PCR
(see the course’s Homepage)