Normal distibution

\(X\) follows a Normal(0,1) iff

\[ℙ(X>a) = \frac{1}{K} \int_{-\infty}^a e^{-\frac{1}{2} x^2} dx\]

Here \(K\) is chosen so total probability is 1

\[K = \int_{-\infty}^\infty e^{-\frac{1}{2} x^2} dx=\sqrt{2\pi}\]

Two independent variables

\[ \begin{aligned} ℙ(X_1>t_1, X_2>t_2) &= ℙ(X_1>t_1) ℙ(X_2>t_2)\\ &= \left(\frac{1}{K} \int_{-\infty}^{t_1} e^{-\frac{1}{2} x_1^2} dx_1\right) \left(\frac{1}{K} \int_{-\infty}^{t_2} e^{-\frac{1}{2} x_2^2} dx_2\right)\\ &= \frac{1}{K^2} \int_{-\infty}^{t_1} \int_{-\infty}^{t_2} e^{-\frac{1}{2} x_1^2} e^{-\frac{1}{2} x_2^2} dx_2 dx_1\\ &= \frac{1}{K^2} \int_{-\infty}^{t_1} \int_{-\infty}^{t_2} e^{-\frac{1}{2} (x_1^2+x_2^2)} dx_2 dx_1\\ &= \frac{1}{K^2} \int_{-\infty}^{t_1} \int_{-\infty}^{t_2} e^{-\frac{1}{2} 𝐱^T𝐱} dx_2 dx_1\\ \end{aligned} \]

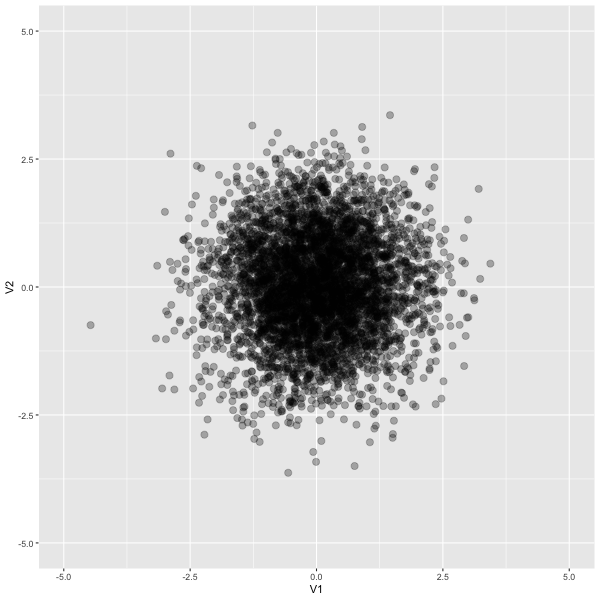
Changing scale

Let \(U_1 = a⋅X_1\) and \(U_2 = d⋅X_2\). What is \(ℙ(U_1, U_2)\)?

Since we have \(X_1 = U_1/a\) and \(X_2 = U_2/d\), we get

\[ ℙ(U_1, U_2) = \frac{1}{K^2} \int\int \exp\left(-\frac{1}{2} (\frac{u_1^2}{a^2}+ \frac{u_2^2}{d^2})\right) \frac{du_1}{a}\,\frac{du_2}{d} \]

We can write

\[ \frac{u_1^2}{a}+\frac{u_2^2}{d} = 𝐮^T\begin{bmatrix} 1/a^2 & 0\\ 0 & 1/d^2\end{bmatrix}𝐮= 𝐮^T\begin{bmatrix} a^2 & 0\\ 0 & d^2\end{bmatrix}^{-1}𝐮 \]

Combinig variables

Let \(U_1 = a⋅X_1 + b⋅X_2\) and \(U_2 = c⋅X_1+d⋅X_2\).
That is

\[ \begin{bmatrix} U_1\\U_2\end{bmatrix} = \begin{bmatrix}a&b\\c&d\end{bmatrix} \begin{bmatrix}X_1\\X_2\end{bmatrix} \]

which we can write as \(𝐮=A𝐱\). Thus \(𝐱=A^{-1}𝐮\)

It looks like this

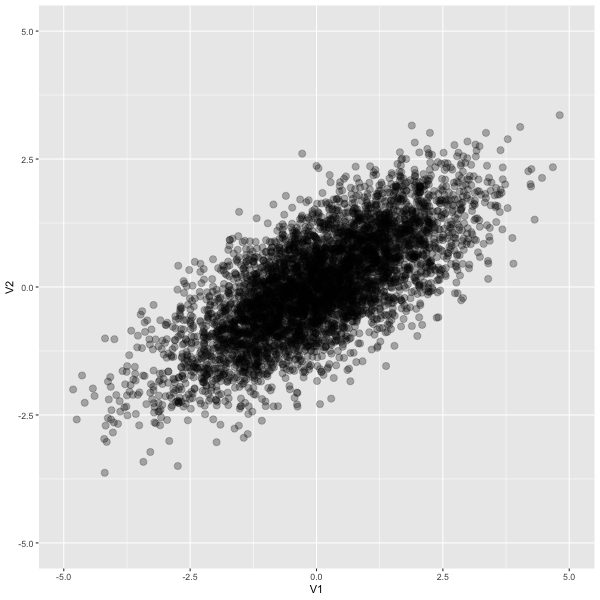
New probability

\[\frac{1}{K^2} \int\int \exp\left(-\frac{1}{2}(A^{-1}𝐮)^T A^{-1}𝐮\right)\det(A^{-1}) du_1\,du_2\] \[\frac{1}{K^2}\det(A^{-1}) \int\int \exp\left(-\frac{1}{2}𝐮^T (A^{-1})^T A^{-1}𝐮\right) du_1\,du_2\]

Determinant

How to calculate 𝐾

Detereminant of product

\[\det(AB)=\det(A)\det(B)\] \[\det(AI)=\det(A) ⇒ \det(I)=1\]

\[\det(A^{-1})=\det(A)^{-1}\]

Trace

Trace of a product

probability again

\[\frac{1}{K^2 \det(A)} \int\int \exp\left(-\frac{1}{2}𝐮^TA^{-T} A^{-1}𝐮\right) du_1\,du_2\] where \(A^{-T}\) is short for \((A^{-1})^T\). Notice that \[(A^{-T} A^{-1})(AA^T)=A^{-T} (A^{-1}A)A^T=A^{-T}A^T=I\] thus \(A^{-T} A^{-1}=(AA^T)^{-1}\)

Naming the new matrix

We will write \(AA^T=Σ\) and then we have \[\det(\Sigma)=\det(A)\det(A^T) = \det(A)^2\] then the probability is

\[ \frac{1}{K^2\det(\Sigma)^{-1/2}} \int\int \exp\left(-\frac{1}{2}𝐮^T\Sigma^{-1}𝐮\right) du_1\,du_2 \]

For more than 2 variables

If we have \(m\) variables (maybe genes) then \(ℙ(U_1,…, U_m)\) is

\[ \frac{1}{K^m\det(\Sigma)^{1/2}} \int\int \exp\left(-\frac{1}{2}𝐮^T\Sigma^{-1}𝐮\right) du_1\ldots du_m \]

\[ \frac{1}{\sqrt{(2\pi)^m\det(\Sigma)}} \int\int \exp\left(-\frac{1}{2}𝐮^T\Sigma^{-1}𝐮\right) du_1\ldots du_m \]

Interpretation

The key part here is \[𝐮^T\Sigma^{-1}𝐮\] This means that the relationship between variables is contained in the matrix \(Θ=Σ^{-1}\)

\(Θ\) is called precision matrix

\(Σ\) is called covariance matrix

So we just need to find the inverse of the covariance

We cannot do that

What we can do instead

Maximum likelihood

Taking logs

divide by \(-n\) (Now we minimize)

\[S=\frac{1}{n}X^T X\]

What we look for

\[\min_\Theta \left(\text{tr}(S\Theta)-\log\det(\Theta)\right)\]

The LASSO trick